The New Rating System of the Korea Baduk Association
Dr. Taeil Bai, MC 4085, Stanford University, Stanford, CA 94305
From January 2009, the Korea Baduk Association (KBA) adopted a new statistical rating system for evaluating the performance of professional baduk (go, weiqi) players. This system was developed by Dr. Bai, a physicist at Stanford University, on the basis of Elo¡¯s rating principles, after analyzing game results of the past nine years (January 2000 - December 2008), in consultation with the Rating Committee of KBA. This system is better than its previous rating system based on bonuses, in the following aspects. It reflects changes of baduk players¡¯ performances in more timely fashion. Additionally, the rating scores are meaningful numbers, which can be analyzed to study progresses of individual baduk players as well as the overall progress baduk players as a population.
1. Basic Equations
As for the winning expectancy function, it adopts the following equation.
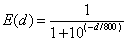
(eq. 1)
Here
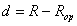
, where R is the player¡¯s rating and

is the rating of the opponent. This equation assumes that one statistical deviation of the distribution of strengths of the go player is 400, which is twice the quantity adopted by the U. S. Chess Federation (ref. 1). The scale of ratings was set such that the rating of the top player is near 9700.
The ratings of players are adjusted each month on the basis of their game results of the previous calendar month, by the following equations.
The rating adjustment for one win is given by
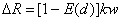
, (eq. 2a)
where E(d) is the winning expectancy of the winner.
The rating adjustment for one loss is given by

, (eq. 2b)
where E(d) is the winning expectancy of the loser.
We can notice two changes are made to the original rating adjustment formula introduced by Dr. Arpad Elo. First, the weighting factor w is introduced to take into account the relative importance of games. The weighting factors are given in Table 1. Second, the term was added to the adjustment formula for a lost game in order to prevent deflation. This term was introduced by Dr. Ales Cieply to the rating system of the European Go Federation (ref. 2). The analysis of previous go games shows that an appropriate choice of the value of satisfactorily prevents deflation. The value of is taken as 0.8, and the k factor is taken as 14.
3. Provisional Ratings
Skill levels of newly licensed professionals are poorly known. However, it is better to include results of games between established and new professionals. It is necessary for this to calculate provisional ratings of new professionals. The provisional rating of a new professional go player is calculated by the following equations, until the number of his (her) games exceeds 30. The rating of a new go player is regarded as established when the number of games exceeds 30, and then the regular adjustment equations are used.
(1) When the number of games is less than 5:

(eq. 3)
where is the rating of the opponent i, n is the number of games, is the number of wins, is the number of losses. Simply said, the provisional rating is obtained by adding 150 point for every win to the average rating of the opponents and subtracting 150 point for every loss from it.
(2) When the number of games is from 5 to 9:
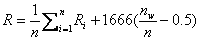
(eq. 4)
This equation assumes the winning expectancy is linear, and the provisional rating becomes the average rating of the opponents plus 833 when he (she) wins all the games.
(3) When the number of games is greater than 9 but less than 30 and all the games are not lost or won, the provisional rating is determined to satisfy the following equation.
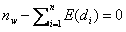
(eq. 5)
Here is the difference between the player¡¯s provisional rating and the rating of the opponent i. There is a unique solution to this equation (in other words, only one value of R satisfies this equation), because and are known. I used the iteration method to find the solution.
(4) The provisional rating is taken to be the average rating of the opponents plus 1170, when the number of games is greater than 9 and less than 30 and all the games are won.
(5) The provisional rating is taken to be the average rating of the opponents minus 1170, when the number of games is greater than 9 and less than 30 and all the games are lost.
The cases for number (3), (4), and (5) are used until the month when the total number of games becomes equal to or more than 30 for the first time. From then, the rating is regarded as established.
Game results played between KBA members and foreign professionals at international tournaments are included for rating calculations. Provisional ratings of foreign players are calculated with the above procedures using the results of games played during the last 36-month period. Once a foreign player plays more than 30 games during any 36-month interval, we use equations (2a) and (2b) to adjust his (or her) rating, regarding the rating as established.
3. The Weighting Factors
The weighting factors are determined by the importance and the stage of the tournament as shown in Table 1. Tournaments are classified as the first, second, and third class tournaments on the basis of the total prize money.
Table 1. Weighting Factors
|
Preliminary
round games |
Main
round games |
Championship
games |
| First Class |
2.0 |
2.5 |
3.0 |
| Second Class |
1.5 |
2.0 |
2.5 |
| Third Class |
1.0 |
1.5 |
2.0 |
4. Rating Results
In order to find appropriate values of k and , I analyzed the game results for the period from January 2000 to December 2008. First, I calculated the initial ratings for January 2001, by applying the iteration method to game results of 2000. Using the initial ratings, I investigated monthly ratings obtained with different values of k and to find their appropriate values.
Figure 1 shows ratings of five players, who are ranked in January 2009 as follows: Kang Dongyoon: 3; Won Sungjin: 4; Park Younghoon: 5, Mok Jinsuk: 6; Choi Chulhan: 8. In this figure, we can find that their ratings vary dynamically from month to month. We can see that Choi Chulhan recovered in 2008 from a spell of a big slump started in the middle of 2007. We can also find that Kang Dongyoon, who is ranked third now, rapidly improved in 2007. These show that the k value has been chosen adequately to reflect rapid variations of performance of baduk players.

Fig. 1. Ratings of five strong players.
Ratings of top twenty-five players are listed in Table 2. Except for two players, Lee Changho and Cho Hoonhyun, all of them are young players under 30 years of age. Two of them were born in the 1990s, and Park Junghwan, the youngest professional baduk player in Korea, obtained the Tenth Dan title in January 2009.
The longevity of Cho Hoonhyun, who was ranked first from the late 1970s until the mid 1990s, is remarkable. In 1989, Cho obtained the championship at the First Ing¡¯s Cup Tournament, becoming world famous. Lee Changho, after replacing in the mid 1990s his teacher Cho Hoonhyun from the first rank, dominated the go world until recently. He is still ranked second.
The fact that most strong Korean baduk players are youngsters is due to the following historical events. First, Cho Chi-hoon (or Chikun), who went from Korea to Japan to study baduk at a very early age, became the first-ranked player in Japan in the 1980s, increasing the popularity of baduk in Korea. Then, in 1989 Cho Hoonhyun obtained the Ing¡¯s Cup by defeating famous Japanese and Chinese players, propelling the confidence level of Korean baduk players as well as baduk fans. Lastly, in 1991 Lee Changho, then 16 years of age, obtained his first international baduk championship. Especially, the emergence of the 16-year-old baduk prodigy induced many parents with young children to send their kids to baduk schools as an extra-curricula activity. From this large pool of baduk pupils, very talented ones were chosen for concentrated training to become professional baduk players. Therefore, the average skill level of newly licensed professionals increased steadily in recent years.
The ratings of the KBA members range from about 7000 to 9750. This range is about 7 times the standard deviation of the performance distribution. The depth of skill levels of professional baduk players is remarkable, considering that the rating difference between the international chess champion and the chess master (2800-2200) is about 3 times the standard deviation of the player performance. This difference in the depths of skill levels for these two board games with ancient origins is due to the fact that the average number of moves per one baduk game is about 200 (200 half-moves in chess terms). Therefore, in a baduk game, the stronger player has more chances to exploit their skill difference than in a chess game. Additionally, a draw is not possible in competitive baduk games because the advantage of the player who makes the first move is set to be either 5.5 or 6.5, depending on the tournament, while the actual sizes of baduk territories are expressible only in integers.
Table 2. Ratings of Top 25 Players
| Rank |
Name |
Rating |
Year of Birth |
| 1 | Lee Sedol | 9758 | 83 |
| 2 | Lee Changho | 9650 | 75 |
| 3 | Kang Dongyoon | 9595 | 89 |
| 4 | Won Sungjin | 9505 | 85 |
| 5 | Park Younghoon | 9490 | 85 |
| 6 | Mok Jinsuk | 9474 | 80 |
| 7 | Yoon Joonsang | 9444 | 87 |
| 8 | Choi Chulhan | 9430 | 85 |
| 9 | Lee Youngkoo | 9399 | 87 |
| 10 | Cho Hanseung | 9388 | 82 |
| 11 | Park Jungsang | 9387 | 84 |
| 12 | Heo Youngho | 9386 | 86 |
| 13 | Baek Hongsuk | 9337 | 86 |
| 14 | Han Sanghoon | 9324 | 88 |
| 15 | Hong Sungji | 9299 | 87 |
| 16 | Ryu Dongwan | 9298 | 89 |
| 17 | Kang Yootaek | 9291 | 91 |
| 18 | Lee Chungyu | 9285 | 89 |
| 19 | Park Junghwan | 9282 | 93 |
| 20 | Kim Jisuk | 9282 | 89 |
| 21 | Ahn Joyoung | 9272 | 79 |
| 22 | Lee Wondo | 9239 | 89 |
| 23 | Cho Hoonhyun | 9219 | 53 |
| 24 | Kim Hyeongwoo | 9197 | 88 |
| 25 | Park Seunghwa | 9195 | 89 |
5. A Comparison of Theoretical and Actual Winning Rates
The key principle of the Elo rating system is that the winning expectancy is a function of the rating difference. It would be interesting to check how the winning expectancy depends, in practice, on the rating difference. Figure 2 shows the winning rate of higher-rated players as a function of the rate difference. The data are obtained from the results of games played during the four years from 2005 through 2008. Only the games between players who had played 20 or more games during the preceding 12 months are included because ratings of active players are more reliable. First of all, the actual data agree very well with the theoretical values. Differences between theoretical values and actual values are all within statistical uncertainties. The red dot for the first bin represents the outcome of more than 1,600 games, and the one for the twelfth bin, 73 games.
Such a good agreement is due to the fact that Korean professional baduk players are closely connected to each other by games. The number of games played per year by each player ranges from about 15 to 100 games. Therefore, any player who played more than 15 games per year is connected to 90% of other players by only one or two degrees of separation in games, when those who played with each other during one-year period are regarded as separated by one degree.
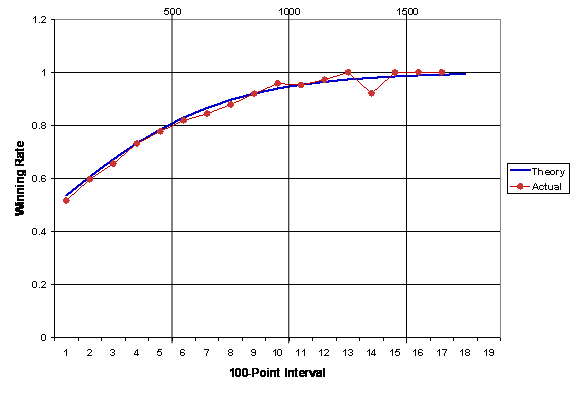
Fig. 2. The winning rate as a function of rate difference.
References
1. Glickman, M. 1995, Amer. Chess J., 3, pp. 59-102.
2. http://gemma.ujf.cas.cz/~cieply/GO/gor.html


